在前面的主题中，我们已经看到了一些重要的概念，例如点荷载作用下简支梁的挠度和斜率，简支梁在均布荷载作用下的挠度和斜率和悬臂梁自由端受点荷载时的挠度和斜率在我们之前的帖子中。
现在我们将从这里开始，在这篇文章中，另一个重要的话题，即悬臂梁的挠度和斜率，在这篇文章的帮助下，在整个梁的长度上均布荷载。
我们已经看到术语和各种术语在最近的柱子的帮助下，用于梁的挠度，现在我们将在这里感兴趣地计算悬臂梁的挠度和斜率，在这个柱子的帮助下，在整个梁的长度上均布荷载。
悬臂梁基本定义为一端固定，另一端自由的梁
．
均布荷载是在梁的长度上分布的荷载，这种荷载的速率在整个梁的分布长度上都是均匀的
基本概念
基本上有三种重要的方法，我们可以很容易地确定受载梁的任何截面的挠度和斜率。
双积分法
力矩面积的方法
麦考利的方法
双积分法和弯矩面积法基本用于确定受载梁在单一荷载作用下任意截面的挠度和斜率。
麦考利法主要用于确定受载梁在多重荷载作用下任意截面的挠度和斜率。
在此我们将使用双重积分法来确定悬臂梁的挠度和斜率，该悬臂梁的整个长度均布荷载。
梁弹性曲线的微分方程将用双重积分法来确定受载梁的挠度和斜率，因此我们必须在这里回忆梁弹性曲线的微分方程．
梁弹性曲线的微分方程
微分方程第一次积分后，我们会得到斜率的值，即dy/dx。同样，微分方程第二次积分后，我们会得到挠度值，即y。
让我们来讨论主要问题，即悬臂梁的挠度和斜率的确定，该悬臂梁的整个长度均布荷载。
让我们考虑一个长度为L的悬臂梁AB，它在支承a处固定，在点B处自由，并承受如下图所示的均布荷载。
我们从上图中得到以下信息，
w =加载速率N/m
AB =悬臂梁在加载前的位置
AB ' =加载后悬臂梁的位置
θ一个=支撑A处倾斜
θB=支撑B处倾斜
yB=自由端挠度
由于udl = W = w.L的总负载
边界条件
我们必须知道在这种问题中适用的边界条件，即梁为
悬臂梁udl
．我们有如下的边界条件。
在点A，挠度为零
在点A处，斜率为零
在点B，挠度最大
在点B，斜率也是最大的
让我们考虑截面XX，距离端支a的距离为x，计算该截面的弯矩。
我们采用符号约定的概念，为上述计算的XX截面弯矩提供了合适的符号。更多关于弯矩符号约定的详细信息，请参阅“弯矩和剪力的符号约定”。
让我们考虑之前确定的关于截面XX的弯矩和梁任意截面的弯矩表达式。我们将得到如下的方程，如下图所示。
现在，我们将对这个方程进行积分，同时，我们将应用边界条件，以确保在梁的某一段的斜率和挠度的表达式，我们可以写出加载梁的斜率和挠度的方程，如图所示。
在那里,C1和C2是积分常数我们可以确定常数C的值1和C2通过对边界条件的考虑和应用。
让我们使用上文所述的边界条件。
在点A，即x =0处，斜率为0，即dy/dx =0
在A点，即x = 0，挠度为0，即y = 0
将上述边坡和梁挠度方程中的边界条件应用后，我们得到常数C的值如下1和C2如前所述。
C1= -王3./ 6
C2=王4/ 24
我们插入C的值1和C2在斜率方程和挠度方程中我们将得到最终的斜率方程以及荷载梁任意截面的挠度方程。斜率方程和挠度方程如下图所示。
自由端斜率
当x = L时，
θB= B端斜率
利用斜率方程，代入x = L，得到支撑B处的斜率，即θB
θB= -
w.L
3.
/ 6 ei
θB= - w。l2/ 6 ei
负号表示B端切线与梁轴AB成逆时针夹角。
最大挠度
在点B即x = L处，挠度最大
我们利用挠度方程，将x = L的值代入挠度方程，就得到了点B的挠度值。
yB= -王4/ 8 ei
yB= - W
l
3.
/ 8 ei
这里的负号表示受力梁的挠度将是向下的。
我们将在下一篇文章中看到另一个主题。
请在本文末尾的评论框中给出你的反馈和建议。
参考:
材料强度，r.k. Bansal著
图片由:谷歌
也读
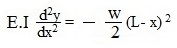
非常好的工作。人们会感谢你的。还有40英尺的低床拖车，知道吗?https://www.dreamtruegroup.com/40ft-low-bed-trailer/
回复删除